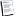
HCl é un acido forte e tenderà a ripristinare l'acido progenitore del sale fluoruro, dunque compare HF che é un acido debole.

HCl(aq) + KF(aq) ---> HF(aq) + KCl(aq)

HF é un acido debole la cui dissociazione

HF(aq) <---> H+(aq) + F-(aq)

costituisce allora un Equilibrio Chimico governato dalla relativa costante d'equilibrio

Ka,HF = |F-| * |H+| / |HF|
Ka,HF = 6.8*10^-4 (aq, 25°C)

Utilizziamo l’equazione di HENDERSON/HASSELBACH

pKa = pH + LOG(|F-| / |HF|)
pKa = 0 - LOG(Ka) = 0 - LOG(6.8E-4) = 3.15..(aq, 25 °C)

da cui si ha

pH = 3.15 + LOG(|F-| / |HF|)

Riarrangiando l'equazione di HH, si ottiene il Rapporto Molare tra F- e HF

|F-| / |HF| = ANTILOG(pH - pKa) = ANTILOG(3.75 - 3.15) = 4

La somma delle rispettive abbondanze molari di F- e HF deve pareggiare l'iniziale contenuto di Acido Fluoridrico

(n,HF) + (n,F-) = (n,F-)° = |KF|° * V° = 1.22 * 550E-3 = 0.67 moli (iniziali) di KF

Così otteniamo un’altra equazione da mettere a sistema
|F-| / |HF| = (n,F-) / (n,HF) = 4
(n,HF) + (n,F-) = 0.67

Risolvendo otteniamo:

(n,F-) = (4 / (1 + 4)) * 0.67 = 0.53 grammo-ioni (finali) di F-
(n,HF) = 0.53 / 4 = 0.13 moli (finali) di HF

Guardando il rapporto stechiometrico notiamo che 1 mole di HCl si consuma ed origina 1 mole di HF

HCl(aq) + KF(aq) ---> HF(aq) + KCl(aq)
Quindi:

(n,HCl) = (n,HF) = 0.13 moli (consumate) di 'HCl'

Ora il volume necessario per irrogare 0.13 moli di HCl è:

V,hcl = (n,HCl) / |HCl|° = 0.13 / 1.3 = 0.10 L